ボリンジャーバンドの計算式をグーグルなどで検索した場合、
多くのサイトでは以下のような計算式が紹介されているはずです。
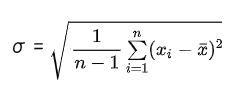
同時に、この計算式は「標準偏差」の計算式である説明があり、
そこで、より詳しくボリンジャーバンドの事を知りたいと思った人は、
「標準偏差とは何なのか」
「この計算式でどのような数値を算出しているのか」
とった事を追って、調べていくのではないかと思います。
ただ「標準偏差」を詳しく解説しているようなサイトは、
統計や確率についての専門的なサイトが大半となっているため、
その分野の専門知識が無い人にとっては難解な説明が施されています。
対して「ボリンジャーバンド」について解説しているサイトでは、
大抵の場合、標準偏差についての説明が不十分である事が多く、
「記事を書いている側も、実はあまりよく分かっていない」
というのが実情なのではないかと思います。
そこで、この記事では統計や確率の専門的な知識が、
ほぼ無いに等しいような人でも「要点」をお分かり頂けるように、
| ・ボリンジャーバンドの計算式にはどのような意味があるのか ・そこで求めてる標準偏差とは、何を意味する値なのか |
といった事を、極力、専門的な話を避ける形で解説していきたいと思います。
| ボリンジャーバンドとは、そもそもどのような指標(インジケーター)なのか、 その基本的な部分は以下の記事で解説していますので併せて参考にしてください。
|
ボリンジャーバンドの計算式の意味と「標準偏差」について。
ボリンジャーバンドは「移動平均線」を中心とする形で、
以下のような「バンド状」の指標が表示されるインジケーターです。
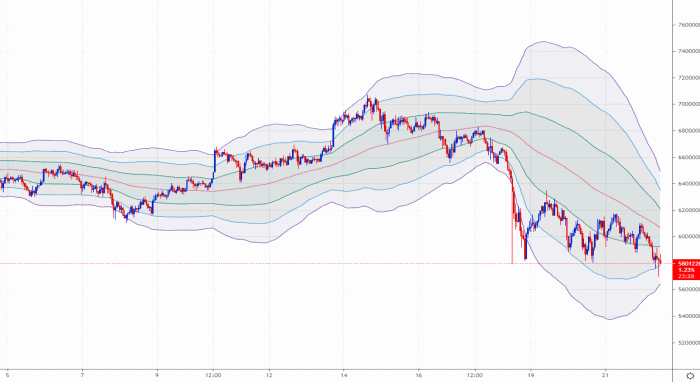
上記の画像で言えば、中央の赤いラインが「移動平均線」であり、
その上下にある最も内側の「緑色のライン」が先ほど示した、
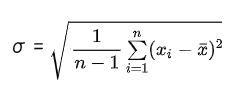
この計算式によって算出される「標準偏差の値の推移」を表しています。
そして、その更に外側にある青色のラインは、標準偏差の2倍の値の推移、
その更に外側にある紫色のラインは、標準偏差の3倍の値の推移を表し、
画像のように「3つのボリンジャーバンド」を併せて表示させるのが一般的です。
↓↓↓
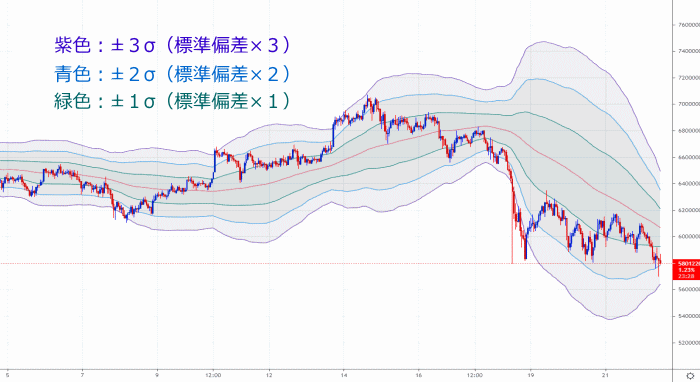
その上で、ボリンジャーバンド(標準偏差)の計算式は、
「一定期間のデータ(レート)のばらつき(散らばり)を数値化するための数式」
であり、この「標準偏差」の計算式で行っている事(計算式の意図)は、
| 1:一定期間の平均値に対して、ばらつきがある終値の差(偏差の値)を算出していく 2:偏差を二乗した値の平均値(分散の値)を算出する(※データ数-1の平均値) 3:偏差を二乗した値の平均値(分散の値)の平方根を取る |
このような4つの段階を踏む計算を1つの計算式にしたものが下記にあたるわけです。
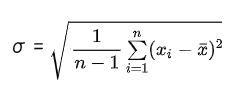
ボリンジャーバンド = 標準偏差の値は、レートの「ばらつき」を示す。
データのばらつきは「平均値に対しての偏り」に他ならないため、
| データ(終値)- 平均値 = 偏差(データの偏り) |
このような計算式でまずは「偏差」と呼ばれるデータの偏りの値を求めています。
計算式の中で言えば下記の赤枠の部分です。
↓↓↓

計算式の中に「∑(シグマ)」のような記号が入ってしまうと、
途端にその計算式の意味が分かりにくくなってしまいますが、
上記の計算式が意味しているのは個々のデータの偏り(ばらつき)にあたる、
「偏差(終値 - 平均値)」
と呼ばれる値を平均値の算出データ(終値)から1つ1つ算出しているわけです。
分かり易い数字で例を挙げると、
| 1日目の終値100円、2日目の終値105円、3日目の110円の相場 |
このような相場の1つ1つのデータ(終値)の「偏差」の値は、
| ・平均レート:(100 + 105 + 110 / 3) = 105円(3日間の平均レート) ・1日目の終値100円の偏差:100円 – 105円(平均レート)= -5円 ・2日目の終値105円の偏差:105円 – 105円(平均レート)= 0円 ・3日目の終値105円の偏差:110円 – 110円(平均レート)= +5円 |
このようになります。
ただ、この時点では個々のデータ(終値)の「ばらつき」を求めた段階のため、
その対象となる期間にどれだけの「ばらつき」があったのかの指針を数値化するには、
これらの「偏差」の値を何らかの合理的な方法で「1つの数値」にする必要があります。
そこで統計においては、個々の偏差を二乗した値の平均値(※データ数-1の平均値)を算出し、
この計算で求めた値が「平均(の値)」に対しての「分散(の値)」とされています。
ここまでが、計算式の中の「√(平方根)」を除いた計算の値となり、
以下の赤枠の「√(平方根)」を外した計算式は「分散の公式:にあたるわけです。
↓↓↓

よって、先ほどと同じ例で「分散」を求めた場合には、
| 1日目の終値100円、2日目の終値105円、3日目の110円の相場 |
| ・平均レート:(100 + 105 + 110 / 3) = 105円(3日間の平均レート) ・1日目の終値100円の偏差:100円 – 105円(平均レート)= -5円 ・2日目の終値105円の偏差:105円 – 105円(平均レート)= 0円 ・3日目の終値105円の偏差:110円 – 110円(平均レート)= +5円 ・分散:(5の二乗 + -5の二乗)/ (3-1) = 12.5 |
このようになるという事です。
何故、個々の偏差を二乗し、データ数から「1」を差し引いて平均値を計算するのか。この「分散の公式」は、なぜ?と思ってしまう部分が多い計算式であり、 ・何故、偏差を二乗して平均する必要があるのか といったところに疑問を感じてしまう人も多いと思います。
これでは指針にならないため「偏差を二乗した平均値」を求める事で、 また「統計」においては、
といった考え方があり ・母集団の標準偏差(および分散)を求める場合の計算式 この2つの計算式は、それぞれの以下のように異なるものになっています。 標本の標準偏差(および分散)を求める場合の計算式 上記の通り、標本の標準偏差を求める場合は「n-1」で偏差の平均を計算しますが、 |
「分散」の値を「標準偏差」へ。
ここまでの解説の中で算出した「分散」の値は算出の際にデータを二乗しているため、
この値をより分かり易い指針としてテクニカル指標などに実用していくには、
「分散の平方根を計算して二乗された単位(数値)を元に戻す」
という計算が必要になります。
ここで、以下のような「標準偏差(標本標準偏差)の計算式」に行き着くわけです。
↓↓↓

先ほどの例で言えば、
| ・平均レート:(100 + 105 + 110 / 3) = 105円(3日間の平均レート) ・1日目の終値100円の偏差:100円 – 105円(平均レート)= -5円 ・2日目の終値105円の偏差:105円 – 105円(平均レート)= 0円 ・3日目の終値105円の偏差:110円 – 110円(平均レート)= +5円 ・分散:(5の二乗 + -5の二乗)/ (3-1) = 12.5 ※「分散」の値では平均レートなどに対して数値を「実用」する事ができない ・標準偏差:12.5の平方根 = 3.5355… |
このようになるため、
| 1日目の終値100円、2日目の終値105円、3日目の110円の相場 |
この3日間の相場のちらばりを示す標準偏差は「3.5355…」という事になります。
この標準偏差の値が大きいほど、平均値の算出対象となった期間において、
レートが大きく変動していた(変動している)事を意味するため、そのような相場は、
平均レートに対して現在レートが乖離する「想定範囲」も広くなるわけです。
↓↓↓
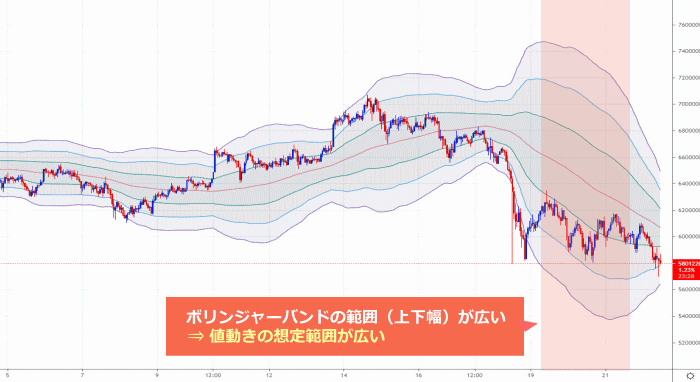
逆に標準偏差の値が小さいほど、平均値の算出対象となった期間において、
レートのばらつきは少なかった(変動が小さかった)事になるため、
平均レートに対して現在レートが乖離する「想定範囲」も狭くなります。
↓↓↓
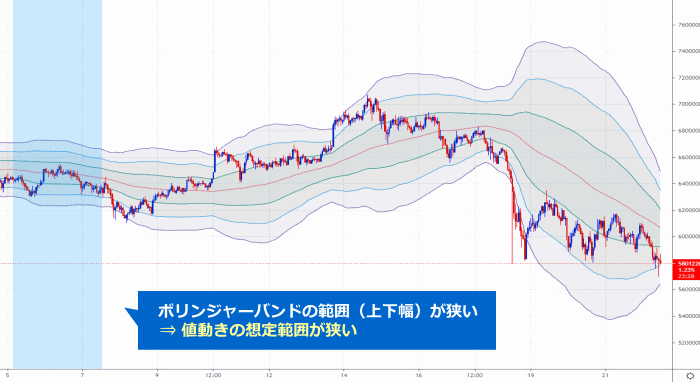
その上で、
| ・標準偏差の「1倍」に相当する範囲(±1σの範囲) ・標準偏差の「2倍」に相当する範囲(±2σの範囲) ・標準偏差の「3倍」に相当する範囲(±3σの範囲) |
これらの「範囲」においては、
| ±1σの範囲内(※上記、緑色のバンド内)で相場が動く確率:68.27% ±2σの範囲内(※上記、青色のバンド内)で相場が動く確率:95.45% ±3σの範囲内(※上記、紫色のバンド内)で相場が動く確率:99.73% |
このような「確率論」が併せて提唱させている傾向にあるものの、
これは統計学の見地において『正規分布』と呼ばれる確率論に基づいた数字が、
ただそのまま何の「根拠」も「裏付け」もなく、漠然と示されているに過ぎません。
確かに、その対象となるデータが『正規分布に基づくデータ』なのであれば、
算出した「標準偏差」の値に対して、上記のような確率論が成り立っていきますが、
『相場の変動値(終値)は正規分布の確率論には基づかない』
という事はハッキリしているため、上記の確率論は相場の値動きには当てはまりません。
つまり、ボリンジャーバンドを解説しているサイトで目にする上記のような確率は、
実際の値動きを統計した上での確率が示されているわけでは無いという事です。
***
よって、ボリンジャーバンドの解説において、実際の相場の値動き(変動)が、
上記の確率論に基づいているかのような内容になっているサイトなどは、
その運営者がボリンジャーバンドの事をあまりよく分かっていない可能性があります。
インターネット上にこの手の記事を書いているような人の大半は、
どこかに書いてあった表面的な情報をただそのまま転載している傾向にあるため、
「その人自身が、その内容や詳細をあまりよく分かっていないのが実情」
という事です。
相場の変動値(終値)は『正規分布』の確率論には基づかない。
何故、相場の変動値(終値)が『正規分布』の確率論には基づかないのか。
その理由を説明するには、そもそもの「正規分布」についてを、
ここで解説した「標準偏差」を踏まえて解説していく必要があるため、
・相場の変動値(終値)が正規分布の確率論には基づかない理由
・相場の終値が99.73%の確率でボリンジャーバンドの範囲に納まらない理由
などについては、以下の記事を併せて参考にしてください。
ただ、上記のような理論解説は「統計」の分野で専門的な話にも及んでしまうため、
「最低限の理屈を踏まえて有効な使い方が分かればそれでいい。」
という場合は、専門的な理論解説を省いた形でボリンジャーバンドの見方や使い方、
それらに基づくトレード判断などを解説している以下の記事を参考にして頂ければと思います。
以上、ここではボリンジャーバンドの計算式と標準偏差について解説させて頂きました。
是非、参考にしてください。
