ボリンジャーバンドは以下のような中心線(移動平均線)の上下に、
「バンド状のラインが表示される形状のインジケーター」
となっています。
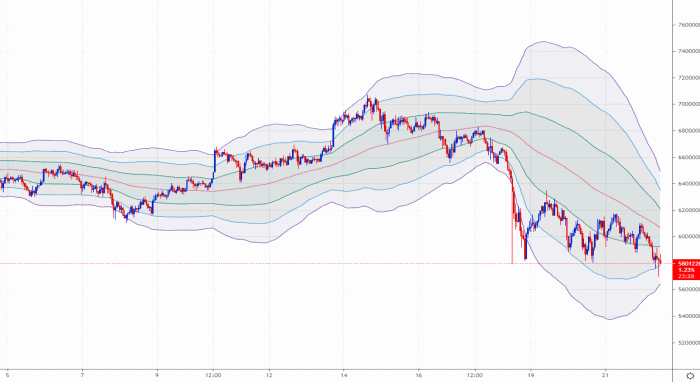
ここでは、この「ボリンジャーバンド」の『見方』や『有効な使い方』を、
その具体的な「ロジック」を踏まえた形で解説していきたいと思います。
ボリンジャーバンドのロジックを踏まえた見方、有効な使い方。
ボリンジャーバンドのロジックの根幹は実質的に「移動平均線」であり、
移動平均線は「平均値をグラフ上に表示していくインジケーター」ですが、
ボリンジャーバンドには、その「内訳」が反映されていく形となっています。
以下がボリンジャーバンドの計算式で、この数式は「標準偏差」と呼ばれる、
「一定期間のデータのばらつき(散らばり)を示す数値」
を算出する「統計」の分野では、かなり頻繁に使われる数式の1つです。
↓↓↓
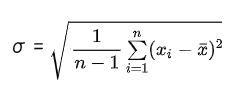
| この計算式の詳細やデータの散らばりを数値化していく「標準偏差」については、 以下の記事で詳しく解説していますので、併せて参考にしてください。
|
よって「ボリンジャーバンド」では、一定期間のレートのちらばり(分散)から、
その時点の平均レートに対して、どれくらいのレートの「乖離」が想定されるのか。
その指針となる「範囲」を『標準偏差』と呼ばれる値に基づいて表示しています。
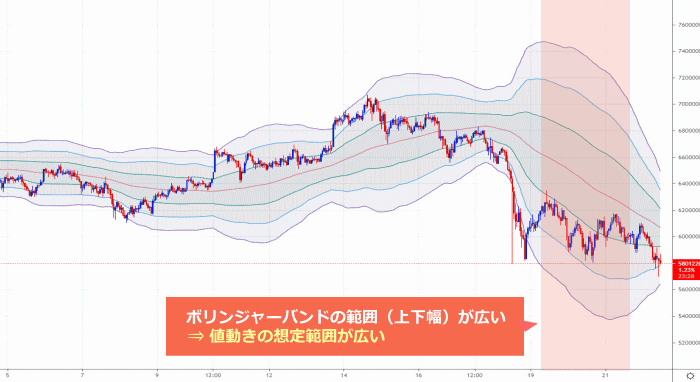
この標準偏差の値が大きいほど、平均値の算出対象となった期間において、
レートが大きく変動していた(変動している)事を意味するため、そのような相場は、
平均レートに対して現在レートが乖離する「想定範囲」も広くなります。
↓↓↓
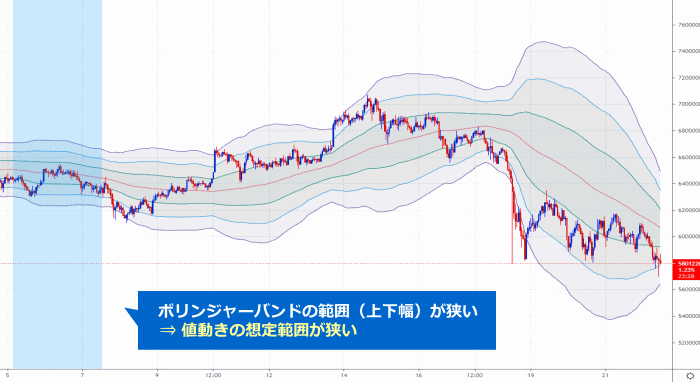
逆に標準偏差の値が小さいほど、平均値の算出対象となった期間において、
レートのばらつきは少なかった(変動が小さかった)事になるため、
平均レートに対して現在レートが乖離する「想定範囲」も狭くなるわけです。
↓↓↓
その上で、ボリンジャーバンドの実質的な「範囲」を示す、
| ・標準偏差の「1倍」に相当する範囲(±1σの範囲) ・標準偏差の「2倍」に相当する範囲(±2σの範囲) ・標準偏差の「3倍」に相当する範囲(±3σの範囲) |
これらの「範囲」においては、
| ±1σの範囲内(※上記、緑色のバンド内)で相場が動く確率:68.27% ±2σの範囲内(※上記、青色のバンド内)で相場が動く確率:95.45% ±3σの範囲内(※上記、紫色のバンド内)で相場が動く確率:99.73% |
このような「確率論」が併せて提唱させている傾向にあるものの、
これは実際の相場の値動きを統計した確率が示されているわけではなく
統計学上の『正規分布』と呼ばれる統計確率がそのまま示されているに過ぎません。
仮に相場の値動き(終値の統計)が『正規分布』に近くなるものなら、
実際の終値の値も上記の『正規分布』に確率に近いものになるのですが、
『相場の変動値(終値)は正規分布の確率論には基づかない』
という事はハッキリしているため、実際の相場の変動(終値)は、
上記の確率の範囲には、全くもって「納まらない」のが現実という事です。
| この『正規分布』の確率論については、
・相場の変動値(終値)が正規分布の確率論には基づかない理由 と共に以下の記事で詳しく解説していますので併せて参考にしてください。
|
相場の終値が99.73%、ボリンジャーバンド±3σの範囲に納まるわけではない。
そもそも「ボリンジャーバンド」を提唱した『ジョン・ボリンジャー』においても、
相場が99.7%、標準偏差±3σの範囲に納まる事を前提とする使い方をしていた事実はなく、
基本的には以下のように「順張り」を前提とする使い方を推進していたと言われています。
↓↓↓
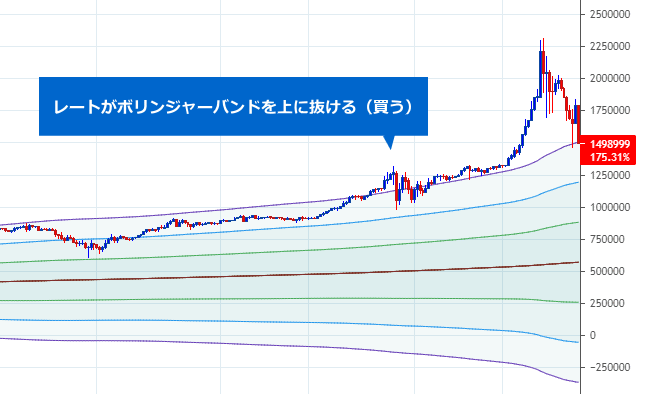
| レートがボリンジャーバンドの上に抜けた ⇒ 相場が大きな「上昇トレンド」に入ったとみて買う |
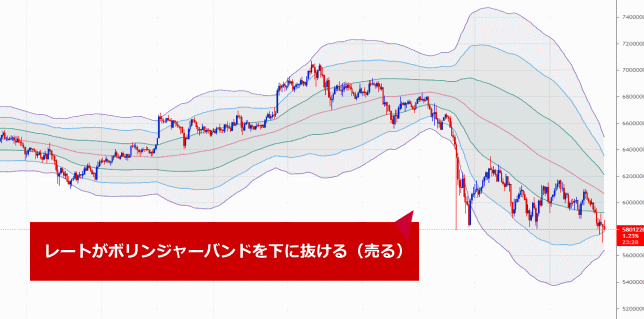
| レートがボリンジャーバンドの下に抜けた ⇒ 相場が大きな「下降トレンド」に入ったとみて売る |
つまり、ボリンジャーバンドによって想定した値動きの範囲を超えたタイミングにおいて、
それを「強いトレンドの発生シグナル」と判断していく形で実用していたわけです。
ですが、
「相場の終値が99.73%の確率でボリンジャーバンドの±3σの範囲内に収まる」
という「誤った統計確率」を真に受けて利用しているようなトレーダーほど、
ジョン・ボリンジャーとは「真逆の使い方」をしている傾向あります。
ボリンジャーバンドの標準偏差±3σのライン前後で「相場の反転」を見越した、
いわゆる「逆張り」のエントリーサインにボリンジャーバンドを使っているわけです。
↓↓↓
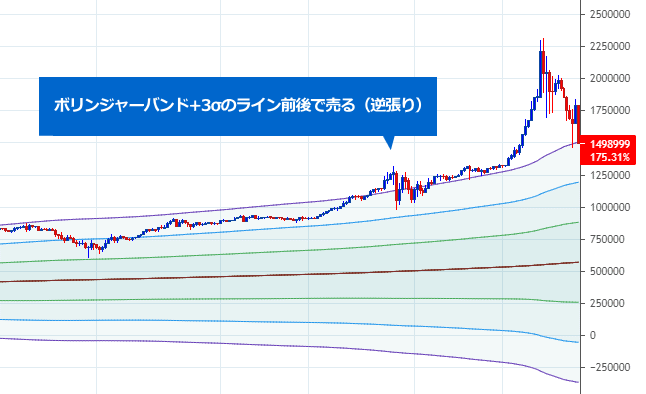
| レートがボリンジャーバンド+3σのラインに接した(抜けた) ⇒ 相場がボリンジャーバンドの範囲内に戻るとみて売る |
↓↓↓
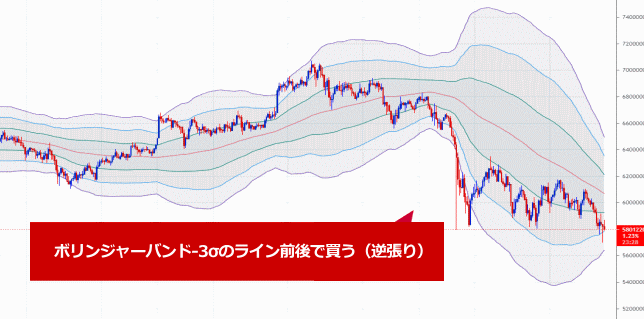
| レートがボリンジャーバンド-3σのラインに接した(抜けた) ⇒ 相場がボリンジャーバンドの範囲内に戻るとみて買う |
もちろん、このような使い方が有効となる場合もありますが、
その使い方で99.73%勝てるのかと言えば、まずそのようにはなりません。
そもそも、その確率論には根本的な「誤り」があるからです。
ボリンジャーバンドは「順張り」に使うべきか「逆張り」に使うべきか。
ただ「正規分布」に基づく99.7%という確率はさすがに再現されていませんが、
それでも、ローソク足の終値が標準偏差±3σの範囲に納まる確率はそれなりに高いため、
ボリンジャーバンドを「逆張り」に使う事自体に合理性が無いわけではありません。
単純な「勝率」で言えば、
| ・ボリンジャーバンド±3σのラインを抜けた時点で順張り ・ボリンジャーバンド±3σのラインを抜けた時点で逆張り |
これらは後者の「逆張り」の方が勝てる確率が高くなるはずです。
ですが、相場が「確率的に優位なパターンを崩すようなケース」は、
| ・テクニカルではないファンダメンタル要因が相場に強く働いている ・そのパターン以上の強いテクニカル要因が相場に強く働いている |
このいずれかの可能性が高いため、ボリンジャーバンドの±3σのラインを抜けて、
更に相場がその方向に延びていくケースは、上記に該当する可能性が非常に高いため、
そのような場合においては「逆張り」には、それ相応の「リスク」が伴います。
ただ、そのようなケースの「リスク」は損切りの判断とタイミングで、
実質的にはいかようにも「最小限」に留める事ができますから、
ボリンジャーバンドを『逆張り』に利用する場合には、
| ・相場がそのまま大きく伸びていく可能性を前提とする事 ・その前提を踏まえたリスクヘッジ(損切り)を徹底する事 |
この2つのポイントを意識する必要があるという事です。
その上で、ボリンジャーバンドを提唱した『ジョン・ボリンジャー』は、
「勝てる時には大きく勝てる(利益を伸ばせる)」
という視点で「勝率よりもリターンを重視していく形」で、
ボリンジャーバンドを『順張り』の指針としていたと考えられます。
よって、ボリンジャーバンドを『順張り』を前提に用いる場合には、
| ・確率的には相場が反転して負ける可能性が高い事 ・勝てる時には大きく利益を伸ばして大きなリターンを追及する事 |
このようなポイントを意識する必要があるという事です。
***
また、ボリンジャーバンドのロジックの主軸は「移動平均線」にあるため、
複数の移動平均線をボリンジャーバンドと組み合わせて利用していくことで、
| ・ボリンジャーバンド±3σのラインで相場が反転する可能性 ・ボリンジャーバンド±3σのラインで相場がそのまま進行していく可能性 |
これらの「可能性」を追及していく事が可能になります。
このような「複数の移動平均線を用いた複合分析」などの方法でも、
ボリンジャーバンドを用いた相場分析の精度を高められるという事です。
私が推奨している『FXism及川デイトレ大百科』の及川圭哉さんのトレード手法も、
そのような「移動平均線による複合分析」を前提としたノウハウとなっていますので、
『移動平均線とボリンジャーバンドを使った有効性の高いトレードノウハウ』
に、もし、ご興味があれば、以下の記事も併せて読んでみてください。
***
テクニカル分析については、他にも多くの記事を公開していますので、
是非、他のブログ記事の方も併せて参考にして頂ければと思います。
